# 数据结构与算法 (DataStructureAndAlgorithms)# 注:该笔记使用 C、开发环境为 VS2022# 算法、复杂度:算法 (Algorithm) 是为了解决某类问题而规定的一个有限长的操作序列。
一个算法必须满足以下五个重要特性:
(1) 有穷性 。一个算法必须总是在执行有穷步后结束,且每一步都必须在有穷时间内完成。
(2) 确定性 。对千每种情况下所应执行的操作,在算法中都有确切的规定,不会产生二义性, 使算法的执行者或阅读者都能明确其含义及如何执行。
(3) 可行性 。算法中的所有操作都可以通过已经实现的基本操作运算执行有限次来实现。
(4) 输入 。一个算法有零个或多个输入。当用函数描述算法时,输入往往是通过形参表示的, 在它们被调用时,从主调函数获得输入值。
(5) 输出
拿算法中最经典的高斯算法为例:
求 1~n 的和,有常规的算法:循环实现,与高斯算法,下面是代码实现:
1 2 3 4 5 6 7 8 9 10 11 #include <stdio.h> int main () { int n = 100 ; int sum = 0 ; for (int i = 1 ; i <= n; i++) { sum += i; } cout << sum; return 0 ; }
1 2 3 4 5 6 7 8 #include <stdio.h> int main () { int n = 100 ; int sum = (1 + n) * n / 2 ; cout << sum; return 0 ; }
我们可以注意到,当使用常规算法时,需要执行的语句数会随着整数 n 的变化而变化,成线性相关,当 n 为一万时,那么 sum+=i; 这条语句需要执行的次数就是一万次。而使用高斯算法时,无论 n 的值是多少,sum = (1 + n) * n / 2; 都只会执行一次。
假设每条语句的执行时间都相同,设为 1,则使用常规算法消耗的时间大致可以认为是 n*1,高斯算法消耗的时间大概是 1。
我们通常使用大 O 表示法,来表示一个算法的复杂度,这里可以写为:常规算法 O (n),高斯算法 O (1)
需要注意的是,若是算法中使用了两个循环 (非嵌套),执行了 2n 条语句,我们仍然记为 O (n)
又或者使用了 2,3,4 条语句,只要这个算法的代码实现并不会随 n 变动,我们仍然记为 O (1)
因此,O (2n),O (3n),O (5),这些形式都是错误的。通常有以下几种表达式来描述时间复杂度:
O (1):常量阶
O (log n):对数阶
O (n):线性阶
O (n log n):线性对数阶
O(n2 ):二次方阶
O(2n ):指数阶
O (!n):阶乘阶
对于一个算法,比如排序一组数据:
1 int arr[] = {1 , 3 , 5 , 10 , 9 };
对于这组数据,显然只需要排序一次便能够得到有序数组,但是这并不代表使用的排序算法就是 O (1) 阶的,我们要按照最差的情况来估计,如果是冒泡排序,我们要按照每一次都需要排序来估计,第一次到第 n 次需要的执行的次数分别为 n-1 到 1,所以总执行次数为 n * (n - 1) / 2 也就是 1/2 * n^2 + 1/2 * n - 1/2 次,我们仅取其最大的部分,则冒泡排序的时间复杂度为 O (n2 ) 阶。
冒泡排序:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 #include <stdio.h> void maoPao (int * arr, int arrLen) { for (int i = arrLen; i > 0 ; i--) { for (int j = 0 ; j < i - 1 ; j++) { if (arr[j] > arr[j + 1 ]) { int temp = arr[j]; arr[j] = arr[j + 1 ]; arr[j + 1 ] = temp; } } } } int main () { int arr[] = { 10 , 9 , 5 , 3 , 1 }; maoPao(arr, 5 ); for (int i = 0 ; i < 5 ; i++) { printf ("%d\t" , arr[i]); } return 0 ; }
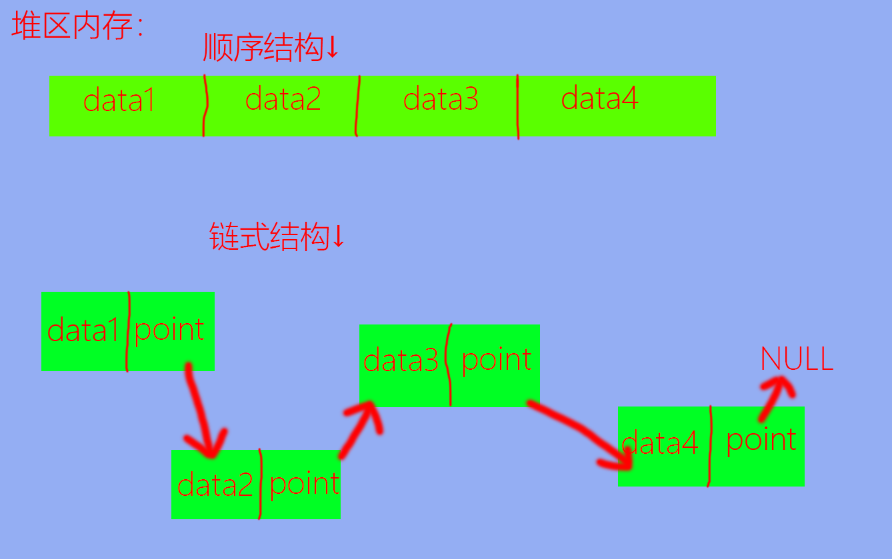
# 顺序结构与链式结构:存储结构大致可以分为两类:
顺序结构:在 物理内存中连续 ,并且在逻辑顺序上也连续 。链式结构:包含 数据域 与指针域 ,在物理内存中不一定连续 ,但在逻辑顺序上连续 。
其中,数据域用于存储数据,指针域用于存储后继元素的地址。
如图:
由图可以直观的看出二者的差别。
顺序结构与链式结构比较:
顺序结构的数据存储密度更高 ,占用空间更少,但是需要一段连续的空间 。
链式结构由于需要使用指针域保存与其关联的节点的地址,所以数据存储密度相对低 ,占用空间更多,但是由于分布存储的特点,并不需要一段连续的空间 。
顺序结构的插入与删除更加繁琐,时间复杂度为 O (n),但是顺序结构的修改,时间复杂度为 O (1)
链式结构的插入与删除,时间复杂度为 O (1),但是查找数据和修改数据,时间复杂度为 O (n)
# 线性结构 # 线性表:线性表(List):零个或多个数据元素的有限序列。
线性表的数据集合为 {a1,a2,…,an},假设每个元素的类型均为 DataType。其中,除第一个元素 a1 外,每一个元素有且只有一个直接前驱元素,除了最后一个元素 an 外,每一个元素有且只有一个直接后继元素。数据元素之间的关系是一对一的关系。
在较复杂的线性表中,一个数据元素可以由若干个数据项组成。在这种情况下,常把数据元素称为记录 ,含有大量记录的线性表又称为文件
# 线性表 - 顺序表1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 #include <stdio.h> #include <stdlib.h> #define OK 0 #define ERROR -1 #define MAX_SIZE 50 typedef int Status;typedef char ElementType;typedef struct List { ElementType data[MAX_SIZE]; int size; int capacity; }List; List* initList () { List* list = (List*)malloc (sizeof (List)); list ->capacity = 0 ; list ->size = MAX_SIZE; return list ; } Status push_back (List* list , ElementType value) { if (list ->capacity == list ->size) { printf ("push error! list is full" ); return ERROR; } list ->data[list ->capacity] = value; list ->capacity++; return OK; } Status push_front (List* list , ElementType value) { if (list ->capacity == list ->size) { printf ("push error! list is full" ); return ERROR; } for (int i = list ->capacity; i > 0 ; i--) list ->data[i] = list ->data[i - 1 ]; list ->data[0 ] = value; list ->capacity++; return OK; } Status insert (List* list , ElementType value, int index) { if (index < 0 || index >= list ->size) return ERROR; for (int i = list ->capacity; i > index; i--) list ->data[i] = list ->data[i - 1 ]; list ->data[index] = value; return OK; } Status pop_back (List* list ) { if (list ->capacity == 0 ) return ERROR; list ->data[list ->capacity] = '\0' ; list ->capacity--; return OK; } Status pop_front (List* list ) { if (list ->capacity == 0 ) return ERROR; for (int i = 0 ; i < list ->capacity - 1 ; i++) list ->data[i] = list ->data[i + 1 ]; list ->data[list ->capacity] = '\0' ; list ->capacity--; return OK; } Status isEmpty (List* list ) { if (list ->capacity == 0 ) return 1 ; return 0 ; } int find (List* list , ElementType key) { for (int i = 0 ; i < list ->capacity; i++) { if (list ->data[i] == key) return i; } return ERROR; } Status pop_by_index (List* list , int index) { if (list ->capacity == 0 ) return ERROR; for (int i = index; i < list ->capacity - 1 ; i++) list ->data[i] = list ->data[i + 1 ]; list ->capacity--; list ->data[list ->capacity] = '\0' ; return OK; } Status DestoryList (List* list ) { free (list ); return OK; } void printList (List* list ) { for (int i = 0 ; i < list ->capacity; i++) { printf ("%c" , list ->data[i]); } } int main () { List* list = initList(); for (char c = 106 ; c > 96 ; c--) { push_front(list , c); } for (char c = 107 ; c < 117 ; c++) { push_back(list , c); } insert(list , 'a' , 10 ); printList(list ); printf ("\n" ); pop_by_index(list , find(list , 'a' )); pop_by_index(list , find(list , 'a' )); push_front(list , 'a' ); pop_back(list ); pop_front(list ); printList(list ); return 0 ; }
# 线性表 - 单链表单链表指指针域中仅仅保存单方向指向后继节点 的指针的链式存储线性表。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 #include <stdio.h> #include <stdlib.h> #define OK 0 #define ERROR -1 typedef int Status;typedef char ElementType;typedef struct Node { ElementType data; struct Node * next ; }Link, Node; Status initLink (Link* link) { link->data = '\0' ; link->next = NULL ; return OK; } Status push_front (Link* link, ElementType value) { Node* newNode = (Node*)malloc (sizeof (Node)); newNode->data = value; newNode->next = link->next; link->next = newNode; return OK; } Status insert (Link* link, ElementType value, int index) { Node* p = link; for (int i = 0 ; i < index; i++) { if (p == NULL ) { printf ("insert error!" ); return ERROR; } p = p->next; } Node* newNode = (Node*)malloc (sizeof (Node)); newNode->data = value; newNode->next = p->next; p->next = newNode; return OK; } Status pop_front (Link* link) { if (link->next == NULL ) { printf ("pop error!" ); return ERROR; } Node* p = link->next; link->next = link->next->next; free (p); return OK; } int find (Link* link, ElementType key) { int index = 0 ; for (Node* p = link->next; p != NULL ; p = p->next) { if (p->data == key) { break ; } index++; } return index; } Status pop_by_index (Link* link, int index) { if (index < 0 ) { printf ("index error!" ); return ERROR; } Node* p = link; for (int i = 0 ; i < index; i++) { if (p == NULL ) { printf ("pop error!" ); return ERROR; } p = p->next; } if (p->next == NULL ) { printf ("pop error!" ); return ERROR; } Node* freeP = p->next; p->next = p->next->next; free (freeP); return OK; } int isEmpty (Link* link) { if (link->next != NULL ) return 1 ; return 0 ; } int sizeofLink (Link* link) { int size = 0 ; for (Node* p = link->next; p != NULL ; p = p->next) size++; return size; } void printLink (Link* link) { Node* p = link->next; while (p != NULL ) { printf ("%c" , p->data); p = p->next; } } ElementType getElem (Link* link, int index) { if (index < 0 ) { printf ("index error" ); return '\0' ; } int count = 0 ; for (Node* p = link->next; p != NULL ; p = p->next) { if (count == index) { return p->data; } count++; } printf ("not found" ); return '\0' ; } Status clearLink (Link* link) { Node* p = link->next; while (p != NULL ) { link->next = link->next->next; free (p); p = link->next; } link->next = NULL ; return OK; } int main () { Link* link = (Link*)malloc (sizeof (Link)); initLink(link); for (int i = 122 ; i > 96 ; i--) { push_front(link, i); } pop_front(link); pop_by_index(link, find(link, 'g' )); printLink(link); insert(link, 'g' , find(link, 'h' )); printf ("\n" ); printLink(link); clearLink(link); printf ("\n" ); printLink(link); return 0 ; }
# 线性表 - 双链表# 栈:# 栈 - 顺序栈1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 #include <stdio.h> #include <stdlib.h> #define OK 0 #define ERROR -1 #define MAX_SIZE 100 typedef int Status;typedef int SElementType;typedef struct { SElementType* base; SElementType* top; int stack_capacity; int stack_size; }Stack; Stack* InitStack () { Stack* stack = (Stack*)malloc (sizeof (Stack)); stack ->base = (SElementType*)malloc (MAX_SIZE * sizeof (SElementType)); stack ->top = stack ->base; stack ->stack_size = MAX_SIZE; stack ->stack_capacity = 0 ; return stack ; } Status Push (Stack* stack , SElementType value) { if (stack ->stack_size == stack ->top - stack ->base) return ERROR; *(stack ->top) = value; stack ->top++; stack ->stack_capacity++; return OK; } Status Pop (Stack* stack ) { if (stack ->top == stack ->base) return ERROR; stack ->top--; stack ->stack_capacity--; return OK; } SElementType GetTop (Stack* stack ) { if (stack ->top == stack ->base) { printf ("Get Error!" ); return ERROR; } return *(stack ->top - 1 ); } Status DestoryStack (Stack* stack ) { free (stack ->base); stack ->base = stack ->top = NULL ; free (stack ); return OK; } int isEmpty (Stack* stack ) { if (stack ->top == stack ->base) return 1 ; return 0 ; } void PrintStack (Stack* stack ) { if (isEmpty(stack )) return ; for (SElementType* sp = stack ->top - 1 ; sp != stack ->base; sp--) { printf ("%d" , *sp); } } int main () { Stack* stack = InitStack(); PrintStack(stack ); for (int c = 10 ; c > -1 ; c--) { Push(stack , c); } while (!isEmpty(stack )) { printf ("%d\t" , GetTop(stack )); Pop(stack ); } DestoryStack(stack ); return 0 ; }
# 栈 - 链栈1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 #include <stdio.h> #include <stdlib.h> #define OK 0 #define ERROR -1 #define MAX_SIZE 100 typedef int Status;typedef int ElementType;typedef struct { ElementType data; struct StackNode * next ; }StackNode; typedef struct { StackNode* next; }LinkStack; LinkStack* InitStack () { LinkStack* ls = (LinkStack*)malloc (sizeof (LinkStack)); ls->next = NULL ; return ls; } Status Push (LinkStack* ls, ElementType value) { StackNode* newNode = (StackNode*)malloc (sizeof (StackNode)); newNode->data = value; newNode->next = ls->next; ls->next = newNode; return OK; } Status Pop (LinkStack* ls) { if (ls->next == NULL ) return ERROR; StackNode* freeP = ls->next; ls->next = ls->next->next; free (freeP); return OK; } ElementType GetTop (LinkStack* ls) { if (ls->next == NULL ) { printf ("Get Error!" ); return ERROR; } return ls->next->data; } Status IsEmpty (LinkStack* ls) { if (ls->next == NULL ) return 1 ; return 0 ; } Status DestoryStack (LinkStack* ls) { StackNode* freeP = ls->next; while (freeP != NULL ) { ls->next = ls->next->next; free (freeP); freeP = ls->next; } free (ls); return OK; } int main () { LinkStack* ls = InitStack(); for (int i = 0 ; i < 10 ; i++) { Push(ls, i); } for (int i = 0 ; i < 5 ; i++) { if (GetTop(ls) != -1 ) printf ("%d\t" , GetTop(ls)); Pop(ls); } DestoryStack(ls); return 0 ; }
# 队列:# 队列 - 顺序结构1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 #include <stdio.h> #include <stdlib.h> typedef int Status;typedef char Element;#define OK 0 #define ERROR -1 #define MAX_SIZE 50 typedef struct { Element data[MAX_SIZE]; int front; int rear; }Queue; Queue* InitQueue () { Queue* q = (Queue*)malloc (sizeof (Queue)); q->front = 0 ; q->rear = 0 ; return q; } int SizeofQueue (Queue* q) { return (q->rear - q->front + MAX_SIZE) % MAX_SIZE; } Status Push (Queue* q, Element value) { if ((q->rear + 1 ) % MAX_SIZE == q->front) return ERROR; q->data[q->rear] = value; q->rear = (q->rear + 1 ) % MAX_SIZE; return OK; } Status Pop (Queue* q) { if (q->front == q->rear) return ERROR; q->front = (q->front + 1 ) % MAX_SIZE; return OK; } Element GetHead (Queue* q) { if (q->rear == q->front) { printf ("Get Error!" ); return '\0' ; } return q->data[q->front]; } Status ClearQueue (Queue* q) { q->front = q->rear = 0 ; } int main () { Queue* q = InitQueue(); for (char c = 97 ; c < 124 ; c++) { Push(q, c); } for (int i = 0 ; i < 26 ; i++) { printf ("%c" , GetHead(q)); Pop(q); } ClearQueue(q); return 0 ; }
# 队列 - 链式结构1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 #include <stdio.h> #include <stdlib.h> #define OK 0 #define ERROR -1 typedef int Status;typedef char Element;typedef struct { Element data; struct QNode * next ; }QNode; typedef struct { QNode* front; QNode* rear; int capacity; }LinkQueue; LinkQueue* InitQueue () { LinkQueue* lq = (LinkQueue*)malloc (sizeof (LinkQueue)); lq->front = lq->rear = NULL ; lq->capacity = 0 ; return lq; } Status Push (LinkQueue* lq, Element value) { QNode* qNode = (QNode*)malloc (sizeof (QNode)); qNode->data = value; qNode->next = NULL ; if (lq->capacity == 0 ) { lq->front = qNode; lq->rear = qNode; lq->capacity++; return OK; } lq->rear->next = qNode; lq->rear = qNode; lq->capacity++; return OK; } Status Pop (LinkQueue* lq) { if (lq->capacity == 0 ) return ERROR; QNode* freeNode = lq->front; lq->front = lq->front->next; free (freeNode); lq->capacity--; return OK; } Element GetHead (LinkQueue* lq) { if (lq->capacity == 0 ) { printf ("Get Error" ); return '\0' ; } return lq->front->data; } Status DestoryQueue (LinkQueue* lq) { QNode* freeNode = lq->front; while (freeNode != NULL ) { lq->front = lq->front->next; free (freeNode); freeNode = lq->front; } free (lq); return OK; } int main () { LinkQueue* lq = InitQueue(); for (char c = 97 ; c < 123 ; c++) { Push(lq, c); } for (int i = 0 ; i < 26 ; i++) { printf ("%c" , GetHead(lq)); Pop(lq); } DestoryQueue(lq); return 0 ; }
# 非线性结构 # 二叉树1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 #include <stdio.h> #include <stdlib.h> #define OK 0 #define ERROR -1 #define NODATA 0 typedef int Status;typedef int ElementType;typedef struct { ElementType data; struct BinaryNode * lchild ; struct BinaryNode * rchild ; }BinaryTree, BinaryNode; BinaryNode* CreateNode () { BinaryNode* bn = (BinaryNode*)malloc (sizeof (BinaryNode)); bn->data = NODATA; bn->lchild = NULL ; bn->rchild = NULL ; return bn; } Status InitTree (BinaryTree* bt) { bt->data = NODATA; bt->lchild = NULL ; bt->rchild = NULL ; return OK; } Status DestoryTree (BinaryTree* bt) { if (bt) { DestoryTree(bt->lchild); DestoryTree(bt->rchild); free (bt); } return OK; } int IsEmpty (BinaryTree* bt) { if (bt->lchild == NULL && bt->rchild == NULL ) return 1 ; return 0 ; } int NodeCount (BinaryTree* bt) { if (bt == NULL ) return 0 ; return (NodeCount(bt->lchild) + NodeCount(bt->rchild) + 1 ); } int Depth (BinaryTree* bt) { if (bt == NULL ) return 0 ; int m = Depth(bt->lchild); int n = Depth(bt->rchild); if (m > n) return (m + 1 ); else return (n + 1 ); } Status InsertTree (BinaryTree* bt, ElementType value) { if (bt->data == NODATA) { bt->data = value; return OK; } if (bt->data > value) { if (bt->lchild == NULL ) bt->lchild = CreateNode(); InsertTree(bt->lchild, value); return OK; } else if (bt->data < value) { if (bt->rchild == NULL ) bt->rchild = CreateNode(); InsertTree(bt->rchild, value); return OK; } return ERROR; } Status PushTree (BinaryTree* bt, ElementType value) { if (bt->data == NODATA) { bt->data = value; return OK; } int l_depth = Depth(bt->lchild); int r_depth = Depth(bt->rchild); if (l_depth <= r_depth) { if (bt->lchild == NULL ) bt->lchild = CreateNode(); PushTree(bt->lchild, value); return OK; } else { if (bt->rchild == NULL ) bt->rchild = CreateNode(); PushTree(bt->rchild, value); return OK; } return ERROR; } void PreorderTraversal (BinaryTree* bt) { if (bt) { printf ("%d\t" , bt->data); PreorderTraversal(bt->lchild); PreorderTraversal(bt->rchild); } } void InorderTraversal (BinaryTree* bt) { if (bt) { InorderTraversal(bt->lchild); printf ("%d\t" , bt->data); InorderTraversal(bt->rchild); } } void PostorderTraversal (BinaryTree* bt) { if (bt) { PostorderTraversal(bt->lchild); PostorderTraversal(bt->rchild); printf ("%d\t" , bt->data); } } int main () { srand((unsigned )time(NULL )); BinaryTree* binary_tree = (BinaryTree*)malloc (sizeof (BinaryTree)); InitTree(binary_tree); InsertTree(binary_tree, 5 ); InsertTree(binary_tree, 9 ); InsertTree(binary_tree, 2 ); InsertTree(binary_tree, 15 ); InsertTree(binary_tree, 3 ); InorderTraversal(binary_tree); DestoryTree(binary_tree); return 0 ; }
# 算法 # 查找# 顺序查找顺序查找是一种十分简单的查找方式,即从第一个数据开始,逐个比对,若查找到目标数据,则返回已查到。若直到结束都未找到,则返回未查找到。
代码逻辑十分简单,这里不再给出代码。
顺序查找的时间复杂度与要找到的数组 (数据库) 长度成线性相关,因此其时间复杂度为 O (n)。
# 二分查找即高中数学中的二分法。
二分查找仅能适用于顺序结构存储的有序数组。
对于有序数组:{21, 24, 64, 74, 83, 215, 456, 982, 7645, 26264};
设置左指针 left=0 指向第一个数 21,右指针 right=10 指向数组尾。
然后取中间值 mid=(left + right) / 2;
如果 arr [mid] 和要查找的目标值相等,则直接返回下标 mid。
如果 arr [mid] 的值大于目标值,那么说明目标值仅可能存在于 arr [mid] 左半侧的数组中 (即小于 arr [mid] 的序列中)。
如果 arr [mid] 的值小于目标值,则说明目标值仅可能存在于 arr [mid] 右半侧的数组中。
这时只需要对于左半侧 (或右半侧) 的数组重复执行上述操作即可。
直到 left 小于 right 时,说明并未查找到目标值,则返回 - 1。
使用 C 语言实现的代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 int BinarySearch (int *arr, int left, int right, int target) { int mid = (left + right) / 2 ; if (left > right) return -1 ; if (target == arr[mid]) return mid; else if (target < arr[mid]) BinarySearch(arr, left, mid - 1 , target); else if (target > arr[mid]) BinarySearch(arr, mid + 1 , right, target); }
通过简单的数学知识可以得出,二分查找的时间复杂度为 O (log2 n)
# 排序算法# 冒泡排序现有待排序数组:arr [10] = { 64, 215, 21, 7645, 24, 456, 74, 83, 26264, 982 };
每次将 arr [i] 和 arr [i + 1] 进行比较,即前一项和后一项比较,如果前者比后者大,则交换其位置 (升序),即:
64 < 215,不交换
215 > 21,交换为 {64,21,215,7645, 24, 456, 74, 83, 26264, 982};
215 < 7645,不交换
7645 > 24,交换为 {64,21,215,24, 7645, 456, 74, 83, 26264, 982};
逐个比较直到最后一个数,这时数组会变成 {64,21,215,24,456,75,83,7645,982,26264};
可以发现,最大的数已经被排到了最后一位,这时不再管最后一个数,将剩余的 9 (n-1) 个数重复上述步骤。
每次都会将第 i 个最大的数排到第 (n - i + 1) 位,当 i=n 时,排序结束。
这样的排序方式,每次都将一个最大 (或最小) 的数排到后面,像是冒泡泡一样,故被称为冒泡排序。
使用 C 语言实现的代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 void BubbleSort (int *arr, int arrLen) { for (int i = arrLen - 1 ; i > 0 ; i--) { for (int j = 0 ; j < i; j++) { if (arr[j] > arr[j + 1 ]) { int temp = arr[j]; arr[j] = arr[j + 1 ]; arr[j + 1 ] = temp; } } } }
冒泡排序每次要遍历的长度为 n,n-1,n-2,n-3…1。
通过等差数列求和公式,可以得出执行次数为 (n+1)*n/2,故冒泡排序是一个时间复杂度为 O (n2 ) 的排序算法。
# 选择排序选择排序是冒泡排序的进阶版本。
可以发现,在冒泡排序中存在着大量的无效交换,如果使用一个下标指针 max,用于记录每次遍历时的最大值,仅在遍历结束时直接将最后一位与最大值进行交换,即可大量减少交换执行的次数。
使用 C 语言实现的代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 void SelectSort (int *arr, int arrLen) { int max = 0 ; for (int i = arrLen - 1 ; i > 0 ; i--) { for (int j = 0 ; j < i + 1 ; j++) { if (arr[j] > arr[max]) max = j; } int temp = arr[i]; arr[i] = arr[max]; arr[max] = temp; } }
从代码可以看出,相较于冒泡排序,选择排序在比较方面并未做出优化,仅优化了交换的代码。
因此选择排序也是一个时间复杂度为 O (n2 ) 的排序算法。
# 插入排序插入排序类似于打牌时,整理手牌的过程。
始终维持一个已经排序好的数组,然后从未排序好的数组中抽一个数,将其插入到已排序数组中的合适位置。
插入时又可以将插入方式分为直接插入 (即从头开始逐个比对,查找合适的位置),和二分插入 (使用二分查找的方式找到一个合适的位置进行插入)。
使用 C 语言实现的代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 void InsertSort (int * arr, int arrLen) { int index = 0 ; int currentValue; for (int i = 1 ; i < arrLen; i++) { currentValue = arr[i]; index = i; while (index > 0 && arr[index - 1 ] > currentValue) { arr[index] = arr[index - 1 ]; index--; } arr[index] = currentValue; } }
插入排序最好的情况是仅有比对,而自身并不移动,最差的情况是从最后一位比对到第一位,并全部都要后移。
时间复杂度为 O (n2 )。
# 谢尔排序 (希尔排序)谢尔排序又名 "缩小增量排序",是插入排序的一种。
当待排序的记录个数较少 (比较次数少),并且待排序的序列基本有序时 (移动次数少),直接插入排序的效率较高。
希尔排序基于以上两点,从 “减少记录个数” 和 “序列基本有序” 两个方面对直接插入排序进行了改进。
现有待排序数组:arr [10] = { 64, 215, 21, 7645, 24, 456, 74, 83, 26264, 982 };
首先设增量 n 为 4,那么把所有间隔为 4 的数字分为一组,可以得到 4 个数组:
{ 64, 24, 26264 };
{ 215, 456, 982 };
{ 21, 74 };
{ 7645, 83 };
然后分别对其进行直接插入排序,最后得到的结果为:
{ 24, 215, 21, 83, 64, 456, 74, 7645, 26264, 982 };
可以发现,相较于一开始的序列,这个序列更有序一些,可以达到减少移动次数的目的。
而对于 4 个数组进行排序时,每个数组的记录个数比原数组也更少,可以达到减少记录个数的目的。
然后将增量 n 减少为 2,那么把所有间隔为 2 的数字分为一组,可以得到 2 个数组:
{ 24, 21, 64, 74, 26264 };
{ 215, 83, 456, 7645, 982 };
然后对其进行直接插入排序。重复这一步骤,直到 n 缩小为 1 时,序列已经基本有序,在执行直接插入排序时便会更快一些。
使用 C 语言实现的代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 void GapInsertSort (int * arr, int arrLen, int start, int gap) { for (int i = start + gap; i < arrLen; i += gap) { int currentValue = arr[i]; int index = i; while (index >= gap && arr[index - gap] > currentValue) { arr[index] = arr[index - gap]; index = index - gap; } arr[index] = currentValue; } } void ShellSort (int * arr, int arrLen) { int n = arrLen / 2 ; while (n > 0 ) { for (int start = 0 ; start < n; start++) GapInsertSort(arr, arrLen, start, n); n /= 2 ; } }
可以看出,谢尔排序的时间复杂度并不稳定,它不仅与数组长度 arrLen 相关,还与分隔子数组时选择的增量 n 相关。
关于增量序列的选择问题,涉及到数学上的一些相关问题,目前还未得到解决。因此,现金并不存在一种最好的增量序列。
有人在大量的实验基础上推出:当 n 在某个特定范围内,谢尔排序所需的比较和移动次数约为 n1.3 ,当 n 趋于正无穷时,比较和移动次数可以减少到 n (log2 n)2
# 快速排序快速排序,我也将其称为中值排序。
现有待排序数组:arr [10] = { 64, 215, 21, 7645, 24, 456, 74, 83, 26264, 982 };
首先选取一个数作为中值,这里选择 arr [0],也就是 64 作为中值
然后设置左标指向序列最左侧,右标指向序列最右侧,然后执行如下操作:
将左标右移,并在移动的过程中将其指向的数与选定的中值比较,遇到大于中值的数时停止。
将右标左移,并在移动的过程中将其指向的数与选定的中值比较,遇到小于中值的数时停止。
将左标与右标所指向的值进行交换,随后重复 1,2。
当左标超过右标时,此刻右标所指的位置,即中值应该存储的位置,将中值与其交换。
这样就将中值放在了 "中间" 的位置,而中值左侧都是小于中值的数,右侧都是大于中值的数。
以中值为界限,将其分为两个数组重复上述操作,直到数组不能再分裂。
使用 C 语言实现的代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 int GetMidIndex (int * arr, int left, int right) { int midValue = arr[left]; int startIndex = left; left++; while (1 ) { while (left <= right && arr[left] <= midValue) left++; while (right >= left && arr[right] >= midValue) right--; if (right < left) break ; else { int temp = arr[left]; arr[left] = arr[right]; arr[right] = temp; } } arr[startIndex] = arr[right]; arr[right] = midValue; return right; } void QuickSort (int * arr, int left, int right) { if (left < right) { int mid_index = GetMidIndex(arr, left, right); QuickSort(arr, left, mid_index - 1 ); QuickSort(arr, mid_index + 1 , right); } }
可以发现,如果每次选取的首个元素都是真正的中值,能够正好将数组等分为两个等长的数组,是最好的情况,此时类似于二分查找。给选取中值查找合适位置的时间复杂度为 O (n),快速排序的时间复杂度为 O (n log2 n)。
最差的情况下,假如每次选取的首个元素,实际上是数组中的最大值 (或最小值),每次都将数组划分为左侧长度为 0,右侧长度为 n-1 (或者右侧长度为 0,左侧长度为 n-1) 的数组,那么快速排序的时间复杂度将退化为 O (n2 ),而且因为算法中使用到递归调用,实际的时间消耗甚至超越冒泡排序。
平均情况下,快速排序是一个时间复杂度为 O (n log2 n) 的排序算法。但它并不稳定。
# 堆排序堆排序是一种树形选择排序,排序过程中,可以将待排序数组看作是一个完全二叉树的顺序存储结构。
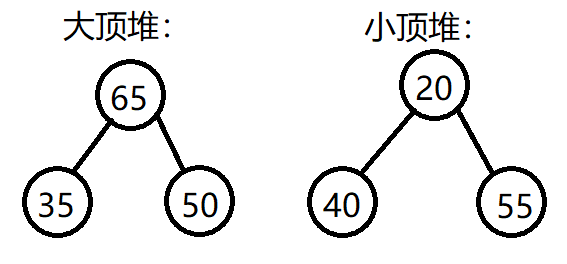
对于二叉树模型,如果根节点的数据大于两个子节点的数据,那么将其称之为大顶堆 (大根堆)。
反之,如果根节点的数据小于两个子节点的数据,那么将其称之为小顶堆 (小根堆)。如图:
对于完全二叉树,有如下性质 (下标按照层次序列):
下标为 i 的节点的根节点下标:(i - 1) / 2
下标为 i 的节点的左子节点下标:i * 2 + 1
下标为 i 的节点的右子节点下标:i * 2 + 2
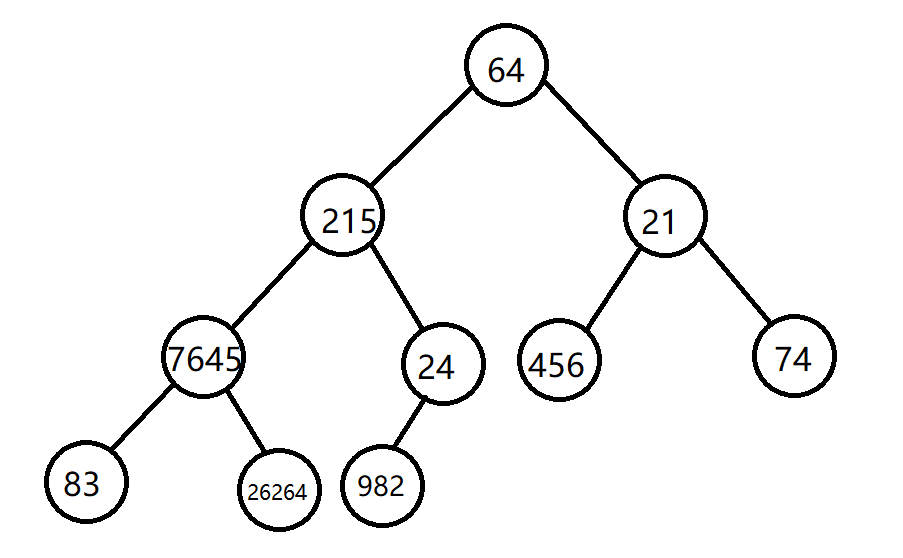
现有待排序数组:arr [10] = { 64, 215, 21, 7645, 24, 456, 74, 83, 26264, 982 };
首先将其构造成完全二叉树:
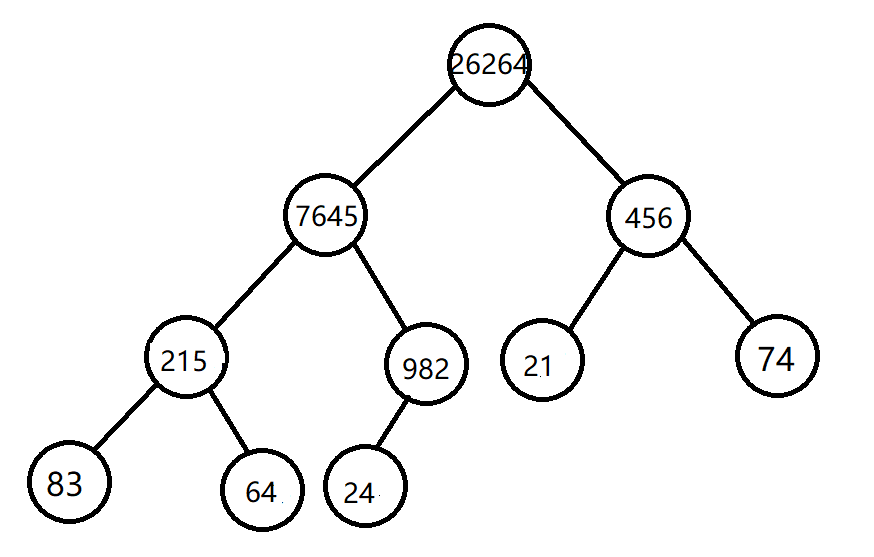
然后将其调整为大顶堆:
此时最大值 26264 已经被交换至根节点,将其输出,然后将 24 交换到根节点处。
然后排除掉已经输出了的 26264。
之所以将 24 交换上去,是为了保证输出 26264 后的数组仍然可以组成完全二叉树。
所以交换至根节点的元素选择,需要保证从下到上,从右到左,这样才能不破坏完全二叉树。
重复构成大顶堆 (或小顶堆),然后输出,交换,直到结束。
使用 C 语言实现的代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 void HeapAdjust (int * arr, int arrLen, int index) { int max_index = index; int l_child = index * 2 + 1 ; int r_child = index * 2 + 2 ; if (l_child < arrLen && arr[max_index] < arr[l_child]) max_index = l_child; if (r_child < arrLen && arr[max_index] < arr[r_child]) max_index = r_child; if (max_index != index) { int temp = arr[index]; arr[index] = arr[max_index]; arr[max_index] = temp; HeapAdjust(arr, arrLen, max_index); } } void HeapSort (int *arr, int arrLen) { for (int i = arrLen / 2 - 1 ; i >= 0 ; i--) { HeapAdjust(arr, arrLen, i); } for (int i = arrLen - 1 ; i > 0 ; i--) { int temp = arr[0 ]; arr[0 ] = arr[i]; arr[i] = temp; HeapAdjust(arr, i, 0 ); } }
堆排序的时间复杂度为 O (n log2 n),其中:
建堆复杂度为 O (n)
维护堆 (HeapAdjust) 复杂度为 O (log2 n)
堆排序对 n 个数进行维护
堆排序的并不是一个稳定的排序算法
# 归并排序归并排序就是将两个或两个以上的有序表合并成一个有序表的过程。将两个有序表合并成一个有序表的过程称为 2 路归并,2 路归并最为简单和常用。
现有待排序数组:arr [10] = { 64, 215, 21, 7645, 24, 456, 74, 83, 26264, 982 };
我们将其分为逐个的单独元素 {64};{215};{21};{7645};{24};{456};{74};{83};{26264};{982}; 此时,划分的每个数组已经排序完毕,因为仅有 1 个数时无需排序。
然后已经排序好的数组两两合并,再次排序:{64, 215};{21, 7645};{24, 456};{74, 83};{982, 26264};
重复上述操作:{21, 64, 215, 7645};{24, 74, 83, 456};{982, 26264};
继续归并:{21, 24, 64, 74, 83, 456, 7645};{982, 26264};
最后得到结果:{21, 24, 64, 74, 83, 456, 982, 7645, 26264};
使用 C 语言实现的代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 void Merge (int * arr, int left, int right, int mid, int arrLen) { int * temp = malloc (sizeof (int ) * arrLen); int i = left; int j = mid + 1 ; int k = 0 ; while (i <= mid && j <= right) { if (arr[i] <= arr[j]) temp[k++] = arr[i++]; else temp[k++] = arr[j++]; } while (i <= mid) temp[k++] = arr[i++]; while (j <= right) temp[k++] = arr[j++]; k = 0 ; while (left <= right) arr[left++] = temp[k++]; free (temp); } void MergeSort (int * arr, int left, int right) { if (left < right){ int mid = (left + right) / 2 ; MergeSort(arr, left, mid); MergeSort(arr, mid + 1 , right); Merge(arr, left, right, mid, right - left + 1 ); } }
归并排序的时间复杂度为 O (n log2 n)
# 各种排序算法的比较
排序算法
最好情况
最坏情况
平均情况
空间复杂度
稳定性
冒泡排序
O(n)
O(n2 )
O(n2 )
O(1)
稳定
选择排序
O(n2 )
O(n2 )
O(n2 )
O(1)
稳定
直接插入排序
O(n)
O(n2 )
O(n2 )
O(1)
稳定
二分插入排序
O(nlog2 n)
O(n2 )
O(n2 )
O(1)
稳定
谢尔排序
O(n1.3 )
O(1)
不稳定
快速排序
O(nlog2 n)
O(n2 )
O(nlog2 n)
O(nlog2 n)
不稳定
堆排序
O(nlog2 n)
O(nlog2 n)
O(nlog2 n)
O(1)
不稳定
归并排序
O(nlog2 n)
O(nlog2 n)
O(nlog2 n)
O(n)
稳定
其中冒泡排序,可以在排序时添加变量 exchange,用于记录遍历过程中是否发生交换,如果某次遍历中并未发生一次交换,说明数组已经有序,可以提前结束排序。最好情况下初始数组便是有序的,则只需一次遍历就可以结束,故最好情况时间复杂度是 O (n)。