力扣算法每日一练
记录一下每日一个 LeetCode 算法题
注:题解大多参考官方或评论区给的答案,我只是补了补注释
# 题目
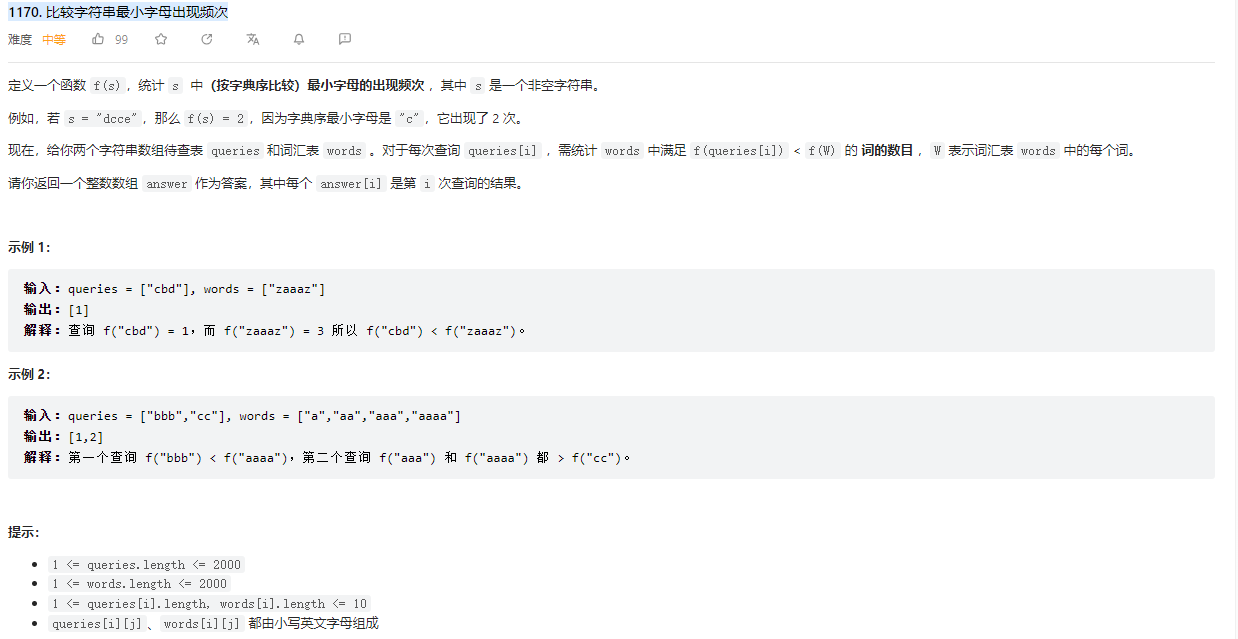
# (1170) 比较字符串最小字母出现频次
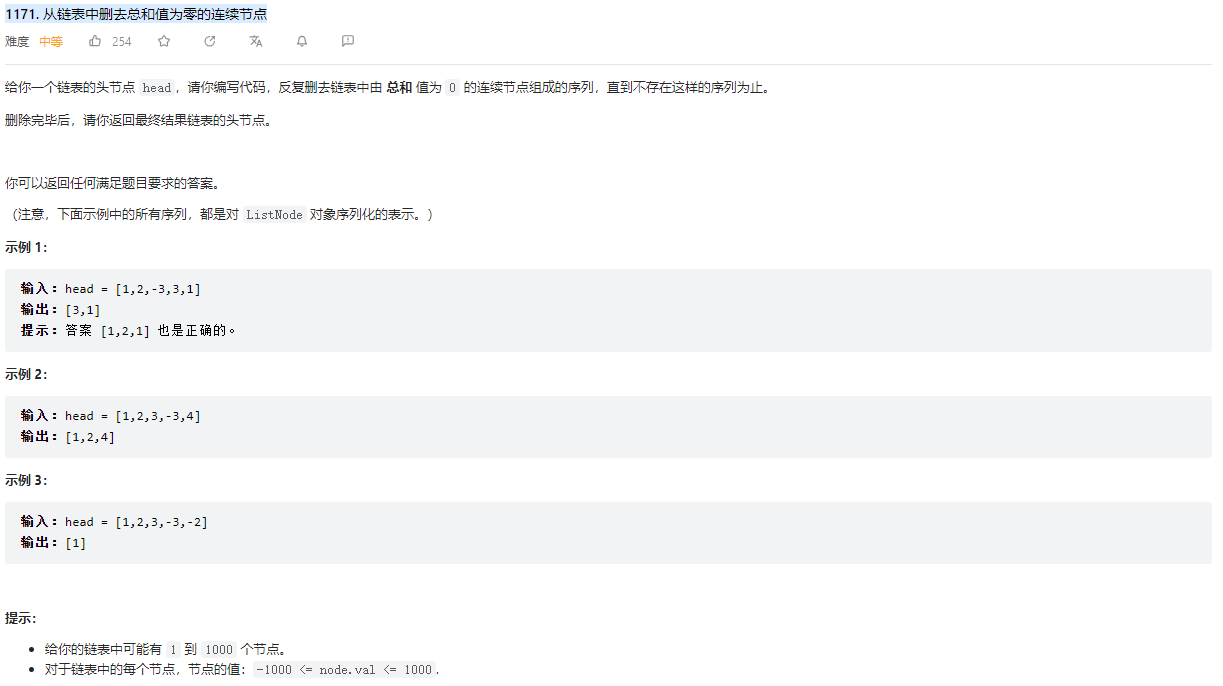
# (1171) 从链表中删去总和值为零的连续节点
# (1483) 树节点的第 K 个祖先

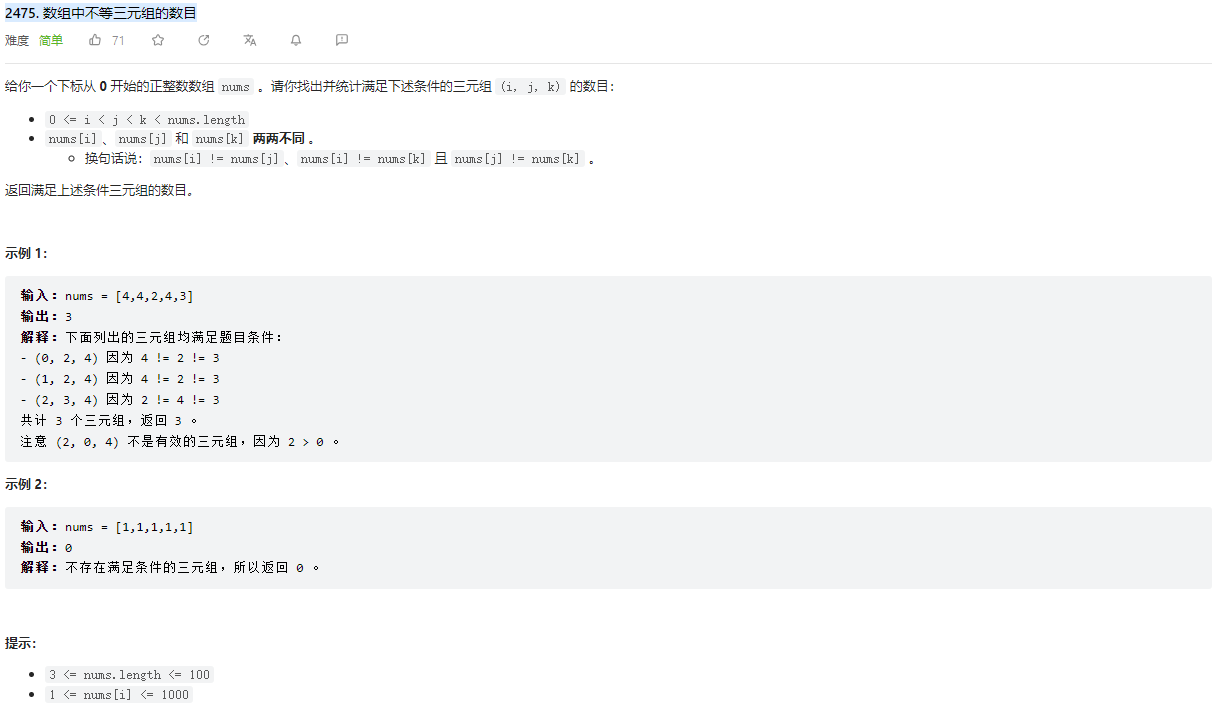
# (2475) 数组中不等三元组的数目
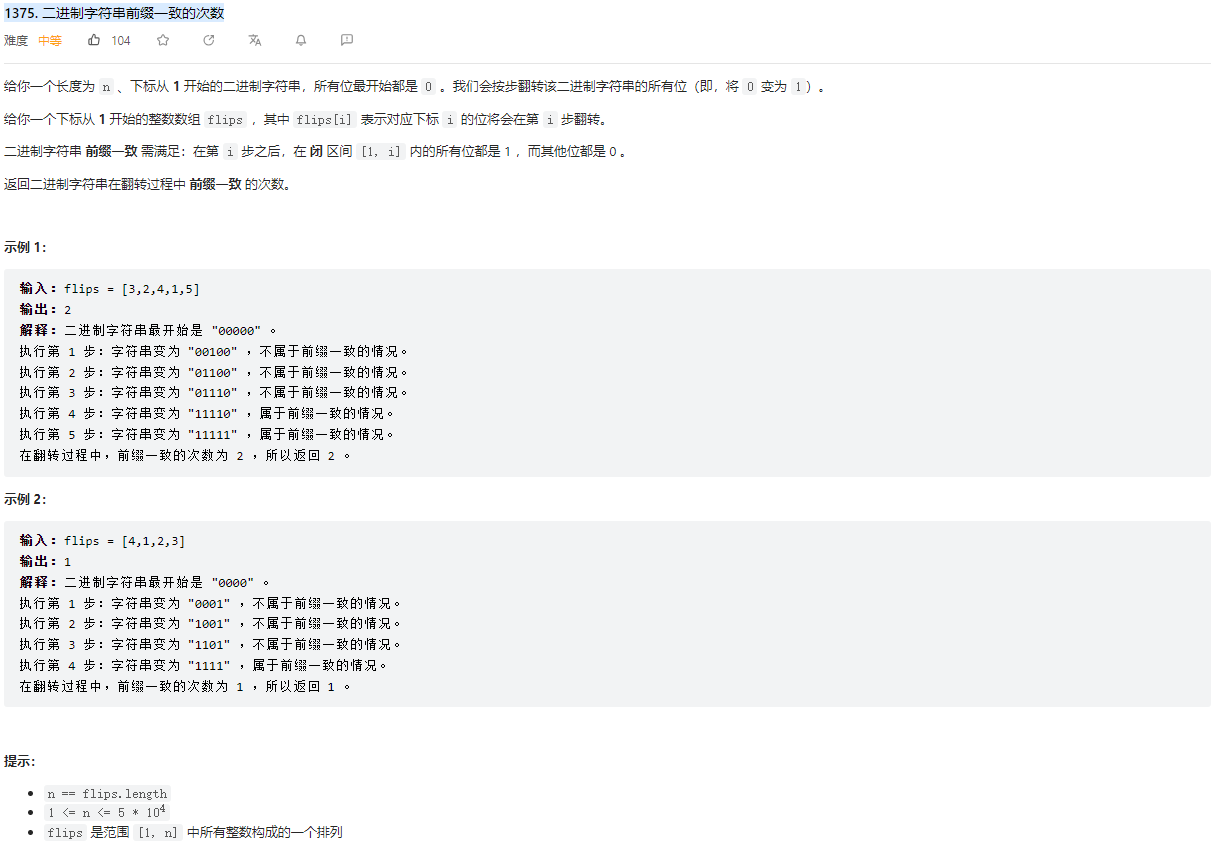
# (1375) 二进制字符串前缀一致的次数
# (1494) 并行课程

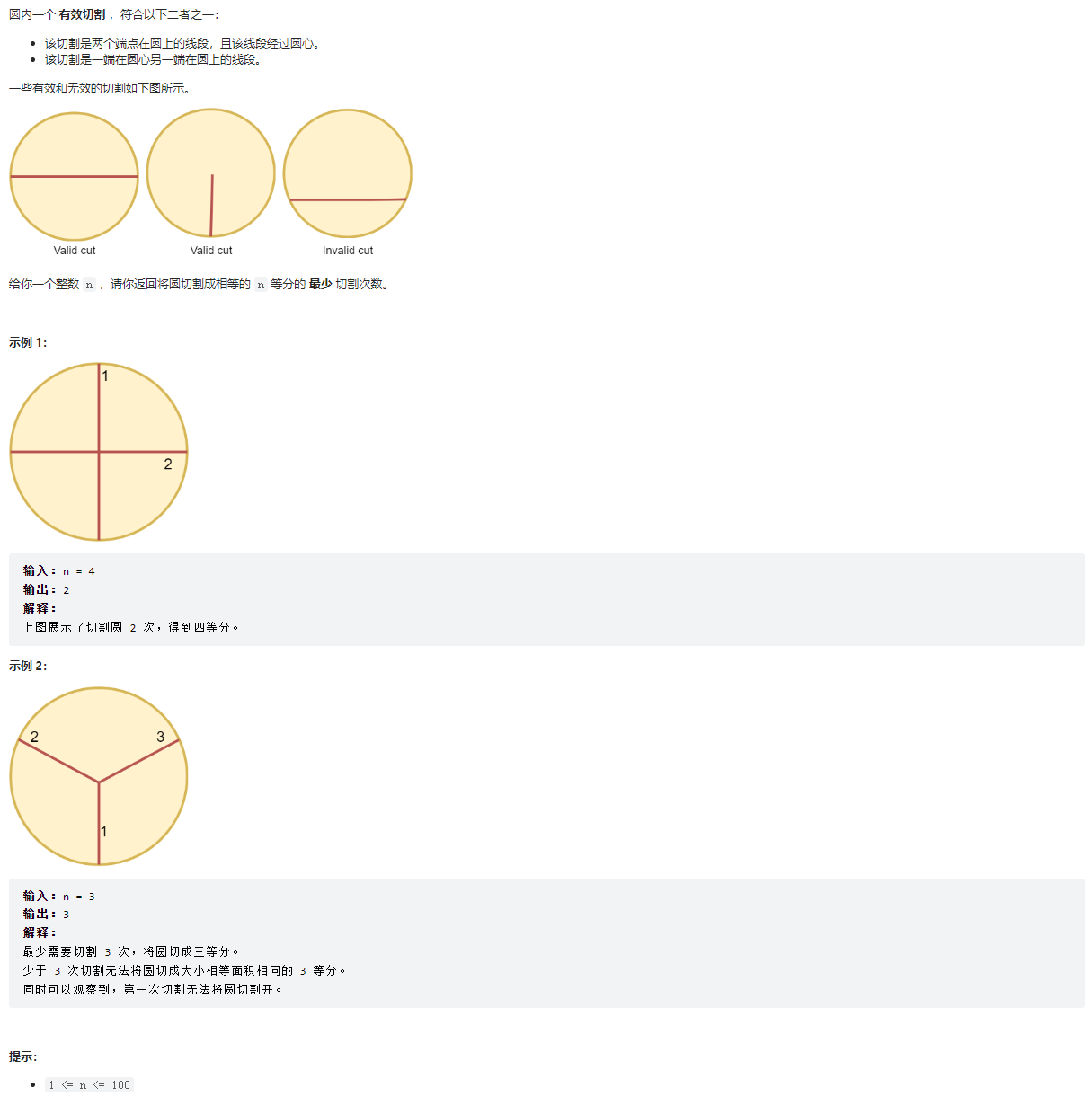
# (2481) 分割圆的最少切割次数
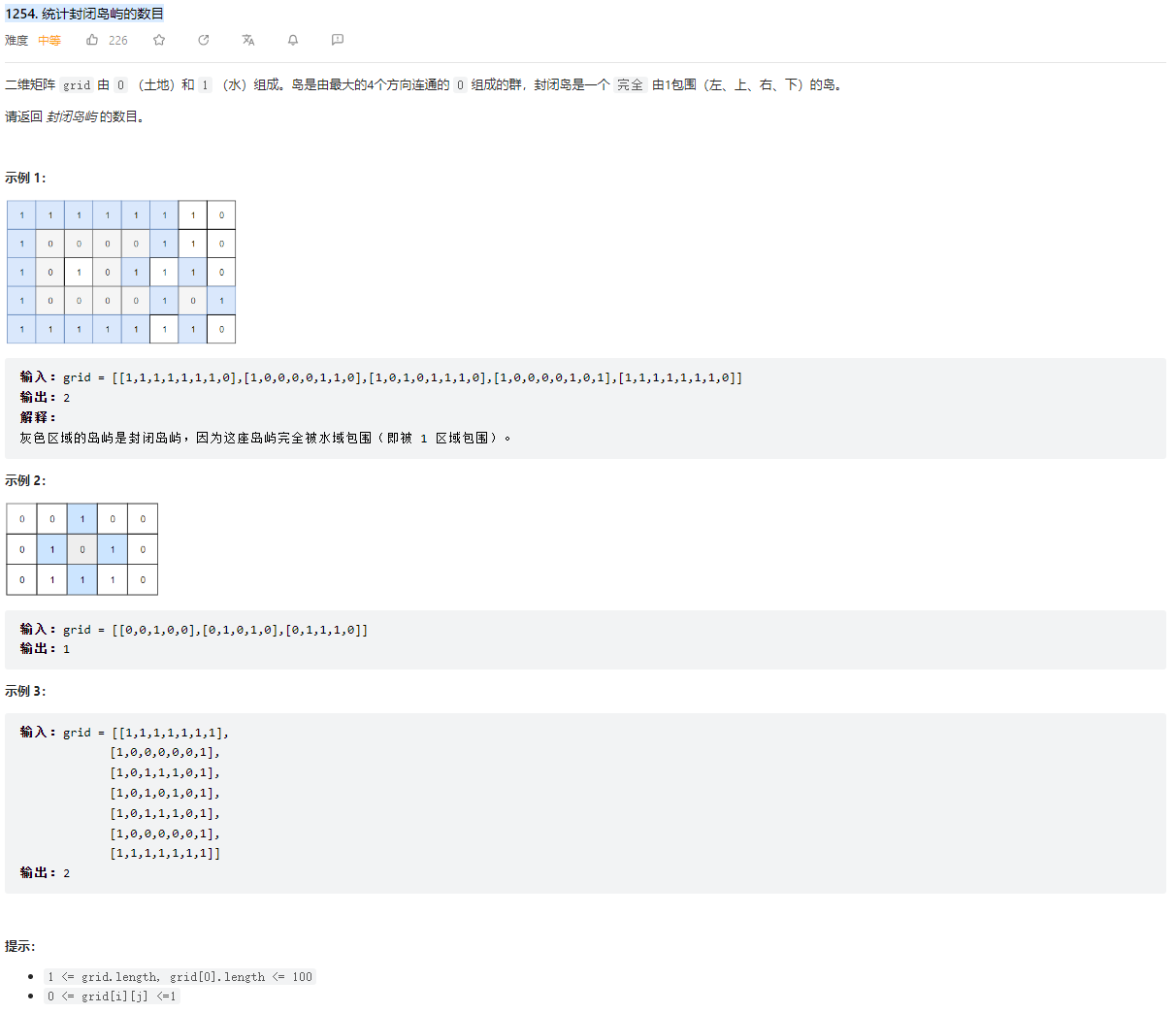
# (1254) 统计封闭岛屿的数目
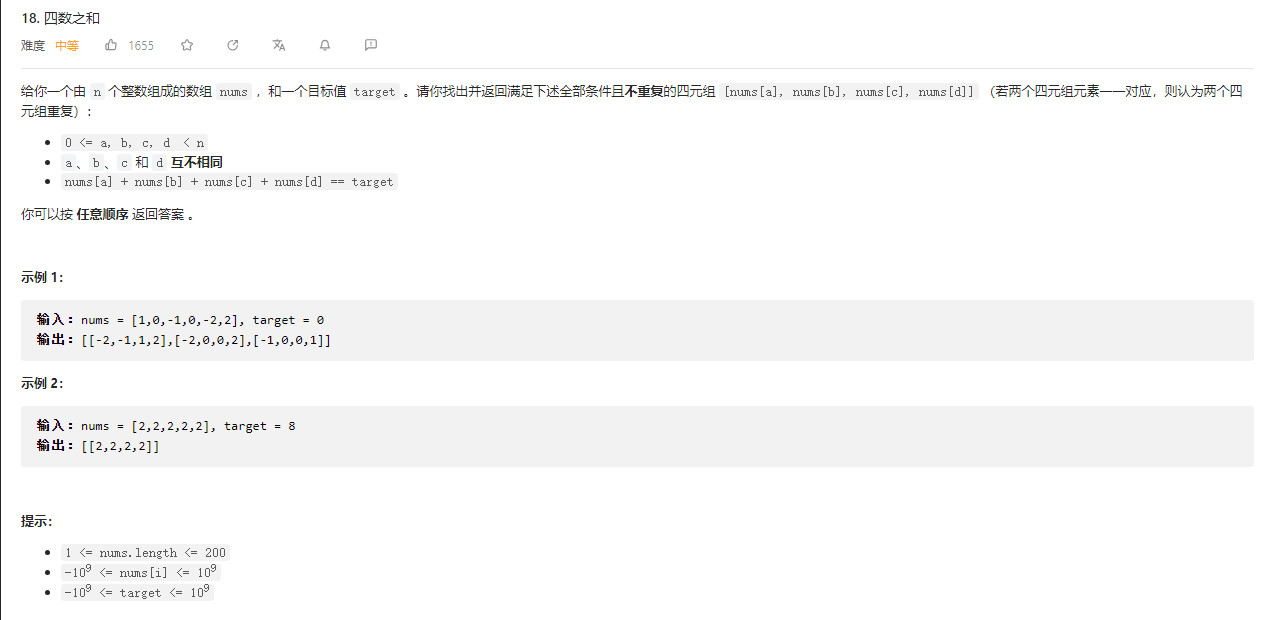
# (18) 四数之和
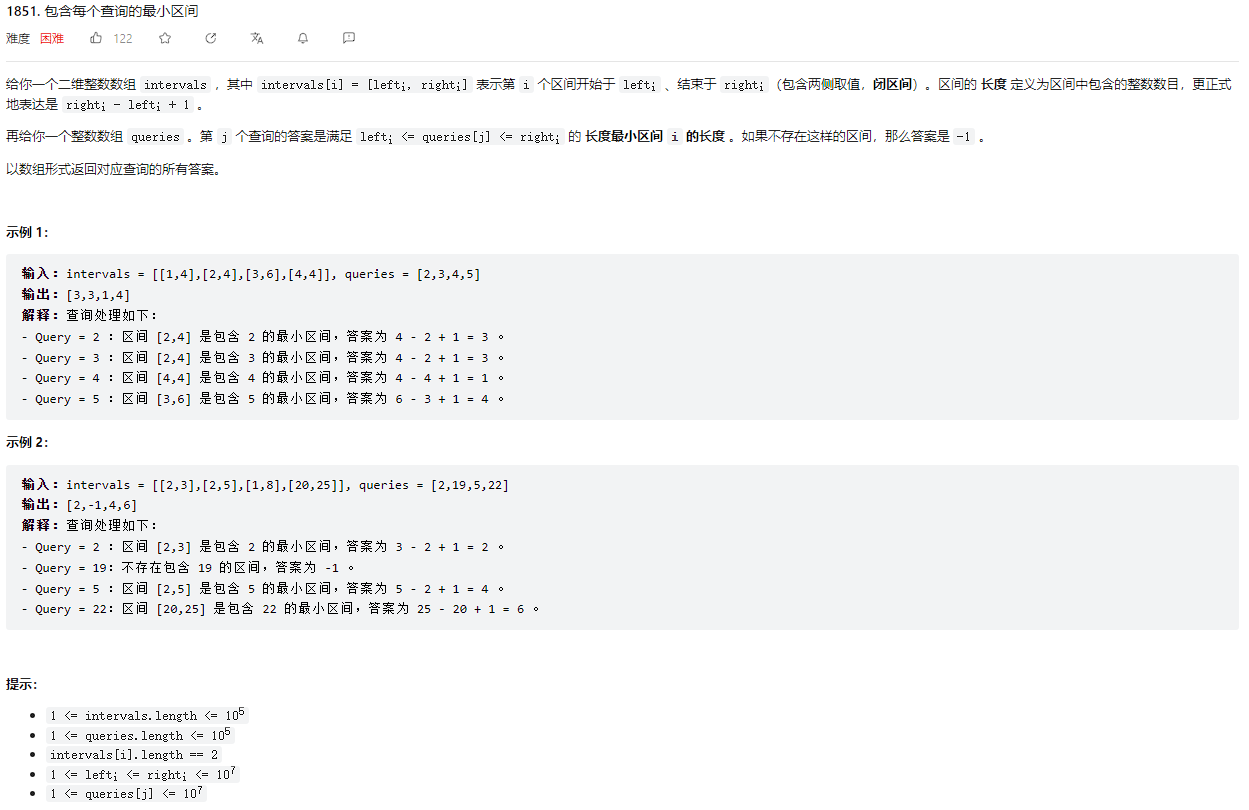
# (1851) 包含每个查询的最小区间
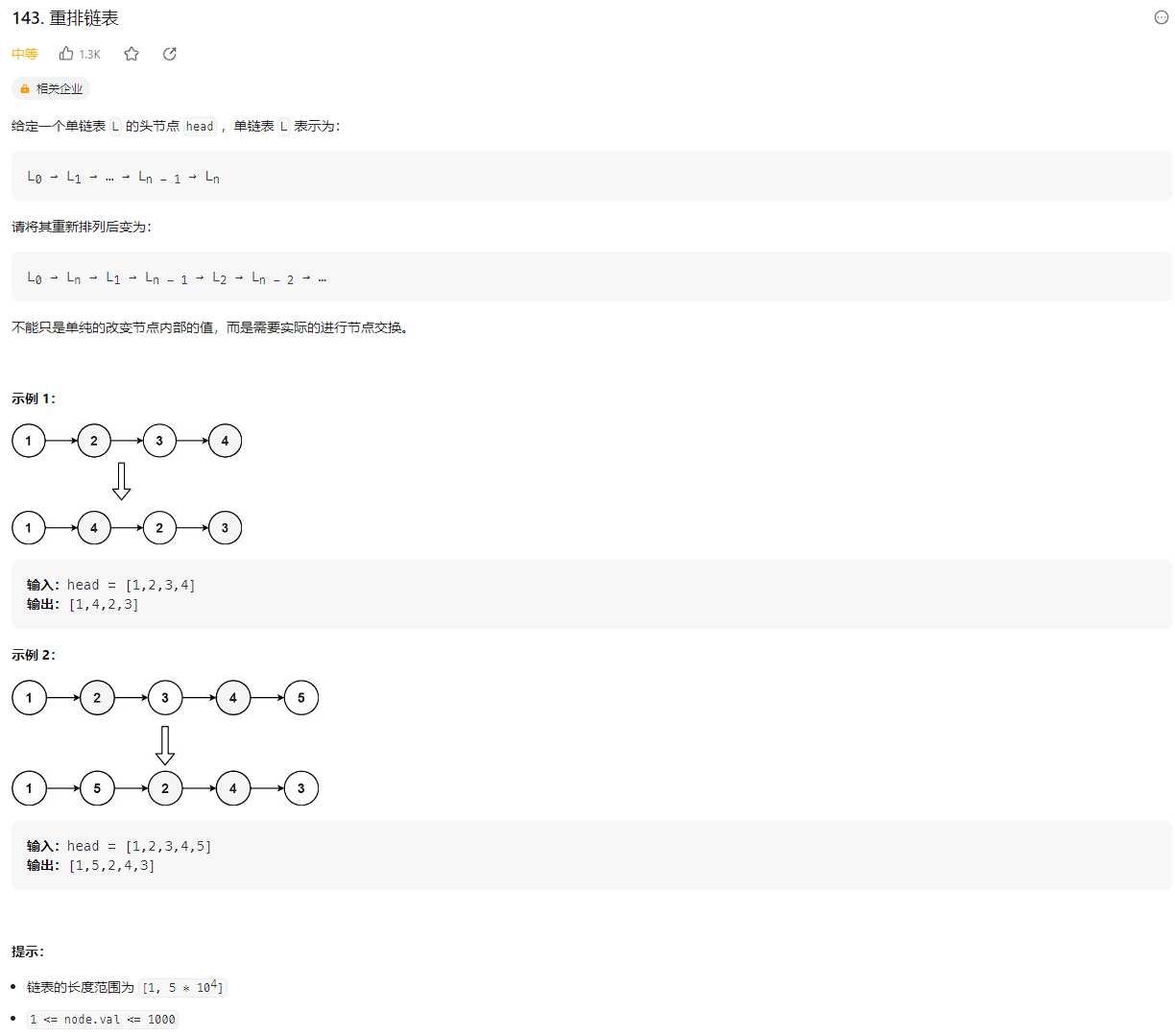
# (143) 重排链表
# (722) 删除注释

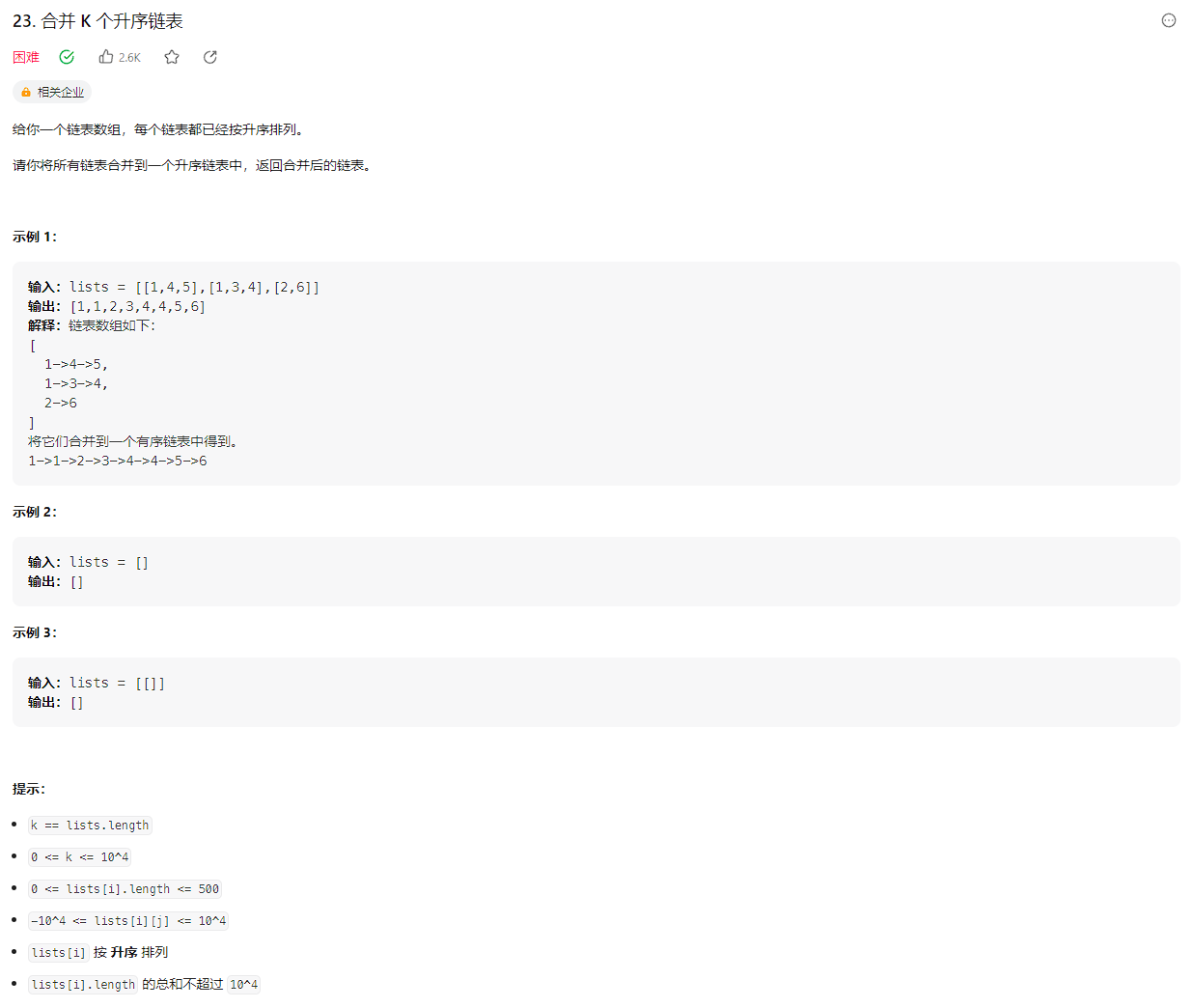
# (23) 合并 K 个升序链表
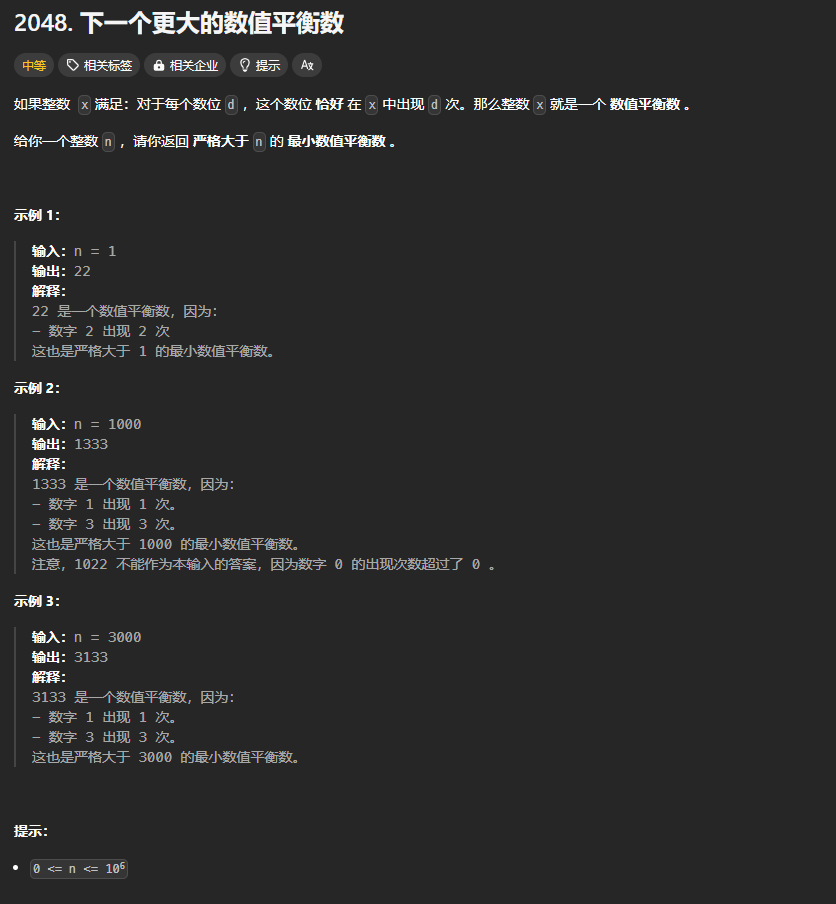
# (2048) 下一个更大的数值平衡数
# 题解
# (1170) 比较字符串最小字母出现频次
1 | class Solution { |
# (1171) 从链表中删去总和值为零的连续节点
1 | /** |
# (1483) 树节点的第 K 个祖先
1 | class TreeAncestor { |
# (2475) 数组中不等三元组的数目
1 | class Solution { |
# (1375) 二进制字符串前缀一致的次数
1 | class Solution { |
# (1494) 并行课程
1 | //答案看不懂,直接复制过来了 |
# (2481) 分割圆的最少切割次数
1 | //纯简单题,没啥好说的,记得考虑n == 1的特殊情况就行 |
# (1254) 统计封闭岛屿的数目
1 | //没看懂0.o |
# (18) 四数之和
1 | //在解决四数之和问题前,我们先来解决其前置题目,三数之和。 |
1 | //理解了三数之和的 排序+双指针 解决方法后,再回来看四数之和的解决方案 |
# (1851) 包含每个查询的最小区间
1 | class Solution { |
# (143) 重排链表
1 | /** |
# (722) 删除注释
1 | class Solution { |
# (23) 合并 K 个升序链表
1 | /** |
1 | //方法2:分治合并 |
# (2048) 下一个更大的数值平衡数
1 |
|
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 Ailzr's Blog!
评论